Accueil > Structures de données et algorithmes >
📚 Algorithmes de recherche classiques
Survol et attentes
Les développeurs sont appelés à trouver des solutions à de nouveaux problèmes, souvent en créant un algorithme sur mesure pour la tâche.
Rechercher une valeur dans une liste est un problème qui connaît déjà plusieurs solutions. Étudier certaines solutions de base vous aide, comme développeur en herbe, à comprendre comment les algorithmes sont structurés et à voir le lien entre un algorithme et la structure de données sous-jacente.
Pour ces types de problèmes, au quotidien, vous utiliserez généralement des solutions optimisées comme les méthodes
containsoubinarySearchdes différents objets de votre langage de programmation.
Définitions
Vous devrez comprendre deux algorithmes de recherche : la recherche séquentielle et la recherche binaire.
- Recherche séquentielle (ou linéaire)
- Une algorithme qui traverse la collection jusqu’à ce qu’il atteigne la valeur cherchée ou la fin de la collection. Des variantes incluent des algorithmes qui traversent toujours la collection entière pour trouver la position de toutes les correspondances avec la valeur cherchée.
- Recherche binaire
- Un algorithme qui divise une collection triée en 2 à chaque comparaison, arrêtant quand la valeur cherchée se trouve au point milieu de la partie restante ou quand il ne reste plus d’items à vérifier. C’est important de noter que la collection doit être triée pour que cet algorithme fonctionne.
Objectifs d’apprentissage
À la fin de cette leçon vous devrez être en mesure de :
- Différencier la recherche séquentielle avec la recherche binaire selon des descriptions, du pseudocode, des diagrammes ou des exemples d’implémentation.
Critères de succès
- Je suis capable d’expliquer un algorithme de recherche séquentielle ou binaire pour des tableaux.
- Je suis capable d’utiliser la méthode
contains(etindexOfquand elle est disponible) de collections comme les String, ArrayList, HashMap, etc. pour faire une recherche appliquant les algorithmes optimisés dans la bibliothèque standard Java.
Notes
Recherche séquentielle / linéaire
Description
La recherche séquentielle est un algorithme qui traverse une collection jusqu’à ce qu’il atteigne la valeur cherchée ou la fin de la collection. Des variantes incluent des algorithmes qui traversent toujours la collection entière pour trouver la position de toutes les correspondances avec la valeur cherchée.
Pseudocode
RechercheSequentielle(liste, cible)
pour chaque élément dans la liste
si élément = cible
retourner vrai
retourner faux
Diagramme de flux
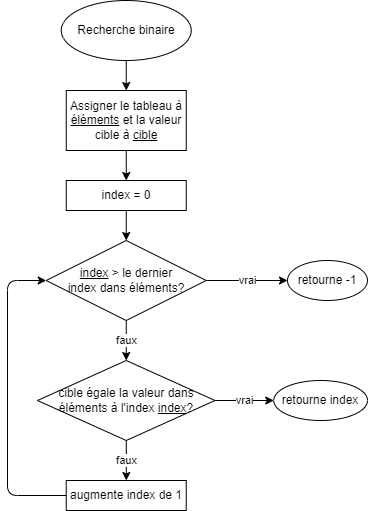
Exemple d’implémentation Java
public static boolean sequentialSearch(int[] elements, int target) {
for (int i = 0; i < elements.length; i++) {
if (elements[i] == target) {
return true;
}
}
return false;
}
Recherche binaire
Description
La recherche binaire est un algorithme qui divise une collection triée en deux à chaque comparaison, arrêtant quand la valeur cherchée se trouve au point milieu de la partie restante ou quand il ne reste plus d’items à vérifier. C’est important de noter que la collection doit être triée pour que cet algorithme fonctionne.
Pseudocode
RechercheBinaire(liste, cible)
gauche = 0
droite = taille(liste) - 1
tant que gauche <= droite
milieu = (gauche + droite) / 2
si liste[milieu] = cible
retourner vrai
sinon si liste[milieu] < cible
gauche = milieu + 1
sinon
droite = milieu - 1
retourner faux
Diagramme de flux
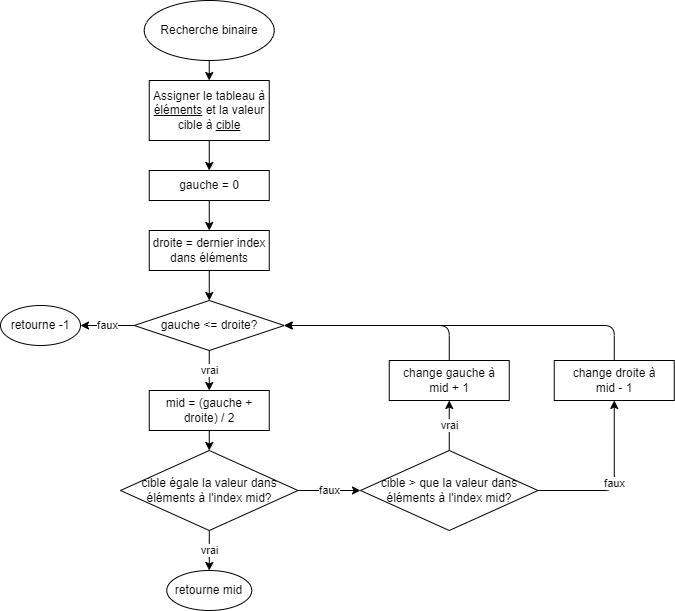
Exemple d’implémentation Java
public static boolean binarySearch(int[] elements, int target) {
int left = 0;
int right = elements.length - 1;
while (left <= right) {
int mid = (left + right) / 2;
if (target == elements[mid]) {
return true;
} else if (target < elements[mid]) {
right = mid - 1;
} else { // target > elements[mid]
left = mid + 1;
}
}
return false;
}
Exercices
Revue interactive - CSAwesome
anglais
Vous pouvez trouvez des vidéos explicatives, des exemples d’implémentations Java et des exercices interactifs en lien avec ce sujet sur le site CS Awesome, notamment la section suivante :
Une recherche séquentielle/linéaire adaptée
Créer un algorithme de recherche séquentielle qui retourne TOUS les index des éléments identiques à la valeur recherchée. Si l’élément n’est pas trouvé, la liste retournée devrait être vide. Vous pouvez utiliser un ArrayList pour stocker les index trouvés.
La signature de la méthode serait alors :
public static ArrayList<Integer> sequentialSearch(int[] elements, int target)
Créez une classe Algos.java pour y mettre cette méthode.
Lancer les tests dans AlgosTest.java (clic-droit et ‘Enregistrer le lien sous’ pour enregistrer le fichier dans votre dossier de projet) pour vérifier votre implémentation. Suivre les étapes 1 à 4 pour ajouter JUnit à votre projet avant de lancer les tests.
Une méthode pour vérifier si un tableau est trié
Créer une autre méthode dans la classe Algos qui vérifie si un tableau d’entiers est trié en ordre croissant. Cette condition est un prérequis pour les algorithmes de recherche binaire.
La signature de la méthode serait :
public static boolean isSorted(int[] elements)
Il devrait retourner true si le tableau est trié et false sinon.
Ajoutez ces tests à votre fichier AlgoTest.java (voir la tâche précédente), à l’intérieur de la classe existante. Mettre le document en forme après le copier-coller pour vérifier que la structure a été maintenue durant l’opération.
@Test
public void testIsSortedWithUnsorted() {
int[] a = { 2, 1, 3, 4, 5 };
assertEquals(false, Algos.isSorted(a));
}
@Test
public void testIsSortedWithEqual() {
int[] a = { 1, 1, 1, 1, 1 };
assertEquals(true, Algos.isSorted(a));
}
@Test
public void testIsSortedWithSorted() {
int[] a = { 1, 2, 3, 4, 5 };
assertEquals(true, Algos.isSorted(a));
}